How to Approach and Solve Math Assignment on Improper Integrals

Dr. Aaron Whitmore

Australia

Math

Dr. Aaron Whitmore, a calculus expert with over 12 years of experience, earned his Ph.D. in Mathematics from Western Sydney University, Australia.

Hire Me To Do Your Math Assignment

To begin, let's clarify what improper integrals are. In integral calculus, we typically deal with proper integrals, where the range of integration is finite, and the integrand (the function being integrated) is bounded in that range. For example, consider the integral:

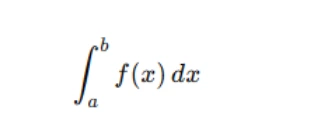
where both the limits a and b are finite, and the function f(x) is well-behaved, meaning it doesn't approach infinity or have any undefined points within the integration range. This type of integral is called a proper integral.

On the other hand, when the limits of integration or the integrand itself become unbounded or undefined, we encounter improper integrals. These can arise in various situations, such as when:

• One or both of the limits of integration are infinite (a=−∞ or b=∞).
• The integrand becomes infinite at a particular point within the range of integration.

Types of Improper Integrals

There are three main types of improper integrals, each of which presents unique challenges:

1. Improper Integrals of the First Kind: These occur when the limits of integration are infinite. For example:



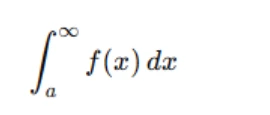
In this case, the function is well-behaved within the finite limits but extends to infinity.

2. Improper Integrals of the Second Kind: These happen when the integrand becomes unbounded at some point within the finite limits of integration. For example:



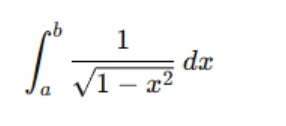
This type of improper integral arises when the function has a singularity at a point within the integration range.

3. 3.Improper Integrals of the Third Kind (Mixed): These integrals combine both of the above types, where the limits of integration are infinite, and the integrand is unbounded at some point within the range. For example:



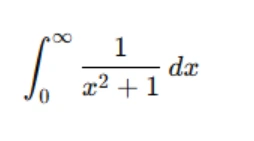
This type of improper integral can be more complex because it combines both behaviors—unbounded limits and an unbounded integrand.

Studying Improper Integrals for Assignments

When tackling assignments involving improper integrals, it is crucial to adopt a systematic approach. Here are some steps that can help you study and solve these types of problems:

• Understand the Theory

Before diving into calculations, ensure you have a solid understanding of the theory behind improper integrals. Know the definitions, types, and the underlying reasons why these integrals arise. This foundational knowledge will help you recognize when you're dealing with improper integrals and how to approach them.

• Break Down the Problem

For improper integrals, breaking down the problem is essential. Start by identifying whether you're dealing with the first, second, or third kind of improper integral. This identification will determine the method you will use for evaluation.

For example, if you're working with an integral where the limits are infinite, you may need to replace the infinite limits with a large number and then take the limit as that number approaches infinity.

• Use Limits to Handle Infinity

Improper integrals often involve infinity, so you’ll need to apply limits to handle this aspect. For integrals of the first kind, where one or both limits of integration are infinite, replace the infinity with a variable (often denoted as RRR) and evaluate the integral. Then, take the limit as R→∞

For example:



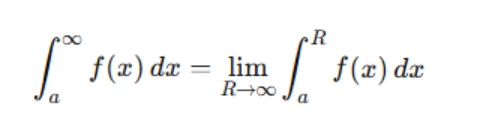
If the limit exists, the integral converges, and you can find its value. If not, the integral diverges, and no finite value can be assigned.

• Deal with Unbounded Integrands

For improper integrals of the second kind, where the integrand is unbounded at a point within the range, you need to carefully handle the singularity. In these cases, split the integral at the point where the integrand becomes unbounded and apply limits to evaluate the behavior near that point.

For instance, for the integral:



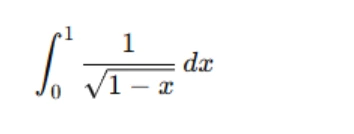
you would need to split the integral at a point close to x=1 (where the function becomes unbounded) and take the limit as x approaches that point.

Common Challenges in Solving Improper Integrals

While the theory of improper integrals is straightforward, the actual computation can be tricky. Here are some common challenges students face when solving these types of integrals:

1. Handling Infinity

Infinity is an abstract concept, and dealing with it can be intimidating. It's easy to become confused when replacing infinity with a variable like RRR and taking the limit as it approaches infinity. This is where a clear understanding of limits becomes crucial.

2. Identifying the Type of Improper Integral

Sometimes, determining whether an integral is improper of the first, second, or third kind can be challenging. It's important to carefully examine the function and the limits of integration to determine the correct classification. If you're unsure, consult your course materials or discuss with your instructor.

3. Evaluating Difficult Integrals

Some improper integrals are complex and may require advanced techniques like partial fraction decomposition, trigonometric substitution, or special integration methods. If you're unsure how to approach a specific integral, reviewing similar examples or seeking guidance from resources like textbooks or online tutorials can be helpful.

4. Divergence

Not all improper integrals converge to a finite value. When solving these integrals, always check the limits to see if they lead to a finite result. If the limit does not exist, the integral is said to diverge, and no finite value can be assigned to it. Recognizing this early on can save time and help you avoid unnecessary calculations.

How to Apply Improper Integrals in Assignments

When applying your understanding of improper integrals to assignments, remember that practice is key. Start with simpler problems and gradually move on to more complex ones as your confidence grows. Here are some tips for solving assignments effectively:

• Understand the Problem Context: Before attempting to solve the problem, carefully read through the assignment question and identify what type of improper integral you're dealing with. Look for clues such as infinite limits or unbounded functions.
• Use the Right Techniques: Depending on the type of improper integral, you will use different techniques (e.g., limit evaluation, substitution). Apply the appropriate methods systematically.
• Check for Convergence: After calculating the integral, always check if the limit exists. If it does, the integral converges, and you can find its value. If the limit doesn't exist, conclude that the integral diverges.
• Consult Resources: If you're struggling, don't hesitate to consult your textbooks, lecture notes, or online resources. Many academic platforms also offer assignment help services that can guide you through difficult problems.

Conclusion

Improper integrals are a challenging but fundamental part of integral calculus. By understanding the different types of improper integrals and applying the right techniques, you can confidently tackle these problems in your assignments. Always approach the problem step by step, use limits to handle infinity, and ensure you check for convergence. With practice, you'll improve your skills and be able to solve even the most complex improper integrals with ease.

By mastering this concept, you'll not only improve your calculus skills but also gain a deeper appreciation for the intricate behavior of functions across infinite domains. Good luck with your studies!