Understanding Linear Equations and Matrices: A Comprehensive Guide for Students

Linear equations and matrices are at the heart of mathematics, and their mastery is a cornerstone of academic success. Whether you're an aspiring mathematician, engineer, computer scientist, or economist, understanding these fundamental concepts is essential. In this comprehensive guide, we'll unravel the world of linear equations and matrices, simplifying complex ideas into manageable components. Our goal is to equip you with the knowledge and tools to not only complete your Linear equations and matrices assignment but also excel in your academic journey.
Imagine approaching your assignments with confidence, knowing that you have a solid grasp of these foundational concepts. Linear equations, which model relationships between variables in a linear fashion, and matrices, which organize and manipulate data efficiently, are skills you'll use repeatedly in your studies and future career. Whether you're just beginning your mathematical journey or seeking a deeper understanding, we've got you covered. From solving linear equations step by step to exploring matrix operations and advanced techniques, this guide will demystify these topics. We'll provide you with the clarity and expertise you need to not only conquer your assignments but also apply these skills to real-world problem-solving scenarios.

So, let's embark on this educational journey together. Whether you're looking to do your matrices assignment or simply aiming to bolster your mathematical prowess, this guide will be your trusted companion, providing insights, examples, and practical advice to help you succeed. Let's dive in and unlock the potential of linear equations and matrices.
Understanding Linear Equations
A linear equation is an algebraic equation that represents a straight line when graphed on a coordinate plane. It has the general form:
ax+by=c
Where:
- a, b, and c are constants,
- x and y are variables.
Linear equations are ubiquitous in mathematics and science, making them a crucial concept to grasp. They are often used to model and solve various real-world problems, such as calculating costs, predicting trends, and determining optimal solutions.
Solving Linear Equations
To solve a linear equation, you aim to find values of x and y that make the equation true. Here's a step-by-step process:
- Isolate the Variable: Begin by isolating one of the variables (usually x or y) on one side of the equation. You can do this by performing operations such as addition, subtraction, multiplication, or division on both sides of the equation.
- Simplify: After isolating the variable, simplify the equation as much as possible.
- Find the Value: Solve for the isolated variable to find its value.
- Check: Always check your solution by substituting the values back into the original equation to ensure it holds true.
Let's work through an example:
3x+2=11
- Isolate x by subtracting 2 from both sides: 3=93x=9
- Simplify: =3x=3
- Check by substituting =3x=3 back into the original equation: 3(3)+2=9+2=113(3)+2=9+2=11 (The equation holds true)
The Versatility of Matrices in Various Fields
Matrices are rectangular arrays of numbers, symbols, or expressions, arranged in rows and columns. They are a fundamental tool in linear algebra and are used to represent and manipulate data in various fields, from computer graphics to statistics. A matrix is denoted as follows:
a_{11} & a_{12} & \cdots & a_{1n} \\
a_{21} & a_{22} & \cdots & a_{2n} \\
\vdots & \vdots & \ddots & \vdots \\
a_{m1} & a_{m2} & \cdots & a_{mn}
\end{bmatrix}\]
Where:
- \(m\) is the number of rows.
- \(n\) is the number of columns.
- \(a_{ij}\) represents the element in the \(i\)-th row and \(j\)-th column.
Matrix Operations
Matrices can be added and multiplied, but these operations follow specific rules:
- Matrix Addition: To add two matrices, they must have the same dimensions (same number of rows and columns). You add corresponding elements together:
- Matrix Multiplication: When multiplying matrices, the number of columns in the first matrix must match the number of rows in the second matrix. The result is a new matrix with dimensions determined by the rows of the first matrix and the columns of the second matrix:
\[C = A + B\]
\[c_{ij} = a_{ij} + b_{ij}\]
\[C = AB\]
\[c_{ij} = \sum_{k=1}^{n} a_{ik}b_{kj}\]
Solving Linear Equations with Matrices
Matrices provide an elegant way to solve systems of linear equations. Consider the following system:
\ [3x + 2y = 11\ ]
\ [x - y = 1\ ]
This system can be represented as a matrix equation \ (Ax = B\ ), where:
\ [A = \ begin{bmatrix}
3 & 2 \\
1 & -1
\ end{bmatrix}\]
\ [x = \ begin{bmatrix}
x \\
y
\ end{bmatrix} \]
\ [B = \ begin{bmatrix}
11 \\
1
\ end{bmatrix}\ ]
\ [Ax = B\ ]
\ [x = A^{-1}B \]
Where \ (A^{-1}\) is the inverse of matrix \ (A\).
Understanding linear equations and matrices not only helps you excel in your assignments but also equips you with valuable problem-solving skills applicable across various disciplines. Whether you're tackling algebraic equations or working with complex data sets, these foundational concepts will serve as powerful tools in your academic and professional journey.
In the following sections, we will delve deeper into solving linear equations with matrices and explore advanced topics that will further enhance your understanding and problem-solving abilities.
Solving Linear Equations with Matrices
Here, we introduced the concept of solving linear equations using matrices. To do this, we utilized the inverse of matrix A to isolate x:
x =A−1 B
Matrix inversion is a powerful tool, but it's important to note that not all matrices are invertible. A matrix is invertible (or non-singular) if and only if its determinant (∣∣∣A∣) is non-zero. In cases where ∣∣=0∣A∣=0, the matrix is singular, and the system of equations may have no unique solution or may be underdetermined.
Gaussian Elimination
Gaussian elimination is an alternative method for solving systems of linear equations. It involves transforming the augmented matrix [A∣B] into a row echelon form (or reduced row echelon form) through a series of elementary row operations. These operations include:
- Swapping two rows.
- Multiplying a row by a non-zero scalar.
- Adding or subtracting one row from another.
The goal is to transform the matrix into an upper triangular form, where the coefficients below the main diagonal are all zeros. Once you have the matrix in this form, you can easily solve for the variables using back-substitution.
Let's illustrate Gaussian elimination with an example:
Consider the system:
2x+3y−z=1
4x+7y+z=3
6x+10y−3z=2
We can create the augmented matrix [A∣B]:
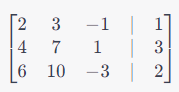
Using Gaussian elimination, we perform row operations to obtain the following row echelon form:

Now, we can back-substitute to find the values of x, y, and z:
From the second row, we have:
y+3z=1
And from the first row, we can express x in terms of y and z:
2x+3y−z=1
2x=1−3y+z
x=21−23y+21z
This method provides a systematic approach to solving linear systems and is particularly useful for larger systems of equations.
Advanced Topics in Linear Equations and Matrices
While mastering the fundamentals of linear equations and matrices is crucial, delving into advanced topics can open doors to even more exciting applications. Advanced concepts like eigenvalues and eigenvectors provide a deeper understanding of transformations and dynamic systems, allowing you to predict behavior and optimize processes in fields ranging from quantum mechanics to machine learning. By exploring these advanced topics, you not only enhance your problem-solving abilities but also position yourself at the forefront of cutting-edge technologies and research. So, while mastering the basics is essential, don't hesitate to venture into the fascinating world of advanced linear algebra for a more profound and rewarding mathematical journey. In this section, we briefly touch upon some advanced concepts:
Eigenvalues and Eigenvectors
Eigenvalues and eigenvectors are advanced concepts that have broad applications in various fields, including physics, engineering, and data analysis. They arise from the study of linear transformations and can be crucial in understanding the behavior of dynamic systems.
- Eigenvalues (λ): Eigenvalues are scalar values associated with a square matrix. For a matrix A, an eigenvalue λ satisfies the equation Av=λv, where v is the corresponding eigenvector. Eigenvalues provide insight into how a transformation scales or stretches space in different directions.
- Eigenvectors (v): Eigenvectors are non-zero vectors that remain in the same direction but may be scaled when multiplied by a matrix. They are essential in understanding the principal directions of transformations.
Applications of eigenvalues and eigenvectors include image compression, stability analysis of dynamic systems, and principal component analysis in machine learning.
Linear Dependence and Rank
Understanding the linear dependence of vectors and the rank of a matrix is vital in various mathematical and scientific contexts.
- Linear Dependence: A set of vectors is linearly dependent if one or more of the vectors can be expressed as a linear combination of the others. Linear independence is crucial for solving systems of equations and determining the dimensionality of vector spaces.
- Rank: The rank of a matrix is the maximum number of linearly independent rows or columns in the matrix. It provides valuable information about the matrix's properties and can be used to determine solutions to linear equations.
Applications in Computer Science and Engineering
Linear equations and matrices find extensive application in computer science and engineering:
- Computer Graphics: Matrices are used to manipulate 3D objects, apply transformations, and render scenes in computer graphics.
- Machine Learning: Linear algebra forms the foundation of many machine learning algorithms. Matrices are used to represent data sets, and linear equations help model relationships between variables.
- Network Analysis: Linear equations and matrices are used to analyze networks, including social networks, transportation systems, and communication networks.
- Control Systems: Linear equations are essential in modeling and controlling dynamic systems, such as robotics and automated processes.
Practical Tips for Mastering Linear Equations and Matrices
Mastering linear equations and matrices may seem daunting, but with the right approach and consistent practice, you can conquer these fundamental mathematical concepts. Remember, these concepts are like building blocks, forming the foundation for more advanced mathematics and their applications in various fields.
Start by grasping the basics of linear equations, understanding how to isolate variables, and honing your problem-solving skills. Practice solving different types of equations to build confidence. As you progress, delve into matrices, recognizing them as powerful tools for organizing and manipulating data. Here are some practical tips to enhance your understanding and excel in solving assignments:
Practice Regularly
Like any skill, mastering linear equations and matrices requires consistent practice. Work through a variety of problems, starting with basic equations and matrices and gradually progressing to more complex ones. Use textbooks, online resources, and software tools to generate practice problems and solutions.
Seek Guidance and Resources
If you encounter difficulties, don't hesitate to seek help. Your instructors, tutors, or peers can provide valuable insights and explanations. Additionally, there are numerous online courses, tutorials, and forums dedicated to linear algebra, offering a wealth of resources and expert guidance.
Build a Strong Foundation
Understanding the fundamentals is essential. Make sure you are comfortable with basic algebraic operations, such as addition, subtraction, multiplication, and division, as these operations are frequently used when solving linear equations and working with matrices.
Visualize and Interpret
Visualization can greatly aid your understanding of matrices and equations. Graphical representations can help you grasp concepts like matrix multiplication and the geometric interpretation of linear equations. Tools like graphing calculators and graph plotting software can be invaluable for this purpose.
Real-World Applications
Explore real-world applications of linear equations and matrices in your field of interest. For instance, if you're studying physics, delve into how matrices are used to describe quantum states. If you're in economics, investigate how linear equations model supply and demand. Understanding the practical applications will deepen your appreciation for these concepts.
Software and Tools
Leverage software packages like MATLAB, Python with NumPy, or R for performing matrix operations and solving linear equations numerically. These tools not only streamline calculations but also provide a practical understanding of how matrices and linear equations are used in modern applications.
Conclusion
In this comprehensive guide, we've explored the fundamentals of linear equations and matrices, from understanding the basics of linear equations to solving complex systems using matrices and methods like matrix inversion and Gaussian elimination.
As a student, these concepts are essential not only for completing assignments but also for building a strong foundation in mathematics and its applications. Whether you're pursuing a degree in mathematics, engineering, or any other field that involves quantitative analysis, the knowledge you've gained here will prove invaluable.
To excel in linear equations and matrices, practice is key. Work through a variety of problems, explore applications in your field of interest, and seek assistance when needed. With dedication and a solid understanding of these concepts, you'll be well-prepared to tackle assignments, excel in exams, and succeed in your academic and professional endeavors. Remember, mathematics is not just a subject; it's a tool that empowers you to solve real-world problems and make a meaningful impact in your chosen field.