Efficient Techniques to Solve Math Assignments Involving Two Variables Functions

Mathematics can be overwhelming when moving from simpler one-variable functions to the more intricate functions of two variables. As university students progress into advanced calculus, mastering these functions becomes essential. Understanding the core principles behind two-variable functions is vital, as they form the foundation for many advanced mathematical concepts. These functions are typically written as f(x,y), where both x and y are independent variables, and the function is evaluated based on their combined effect.
One key concept that comes up frequently in calculus assignments is the limits of functions of two variables. These limits are essential for understanding continuity, differentiability, and optimization problems in multi-variable calculus. Navigating through such concepts involves grasping how functions behave as they approach certain points in a two-dimensional plane. As assignments related to two-variable functions can be tricky, it’s important to break them down into manageable steps, focusing on their limits, derivatives, and potential for critical points.

In this blog, we’ll delve into the challenges often faced in math assignments involving two-variable functions, offering tips and strategies to better approach these problems. By understanding the core concepts of limits and how to solve their math assignment by apply them, students can gain a clearer perspective and confidence in handling such complex topics.
What Are Functions of Two Variables?
Before diving into limits, let's first understand what a function of two variables is. At its core, a function of two variables is similar to a function of one variable, but with an additional layer of complexity. A function z=f(x,y) is a rule that assigns a real number z to every ordered pair (x,y), where both x and y are real numbers.
In simpler terms, while in one-variable functions, we only work with one input (e.g., f(x)), in functions of two variables, the output depends on two separate inputs (e.g., f(x,y)).
Imagine you are standing at a point in a two-dimensional plane, denoted by coordinates (x,y). At each of these points, the function computes a corresponding value z that places a "height" in the third dimension, forming a surface.
The domain of a function is the set of all points (x,y) for which the function is defined, while the range represents the possible output values of z.
Geometric Interpretation of Functions of Two Variables
To better grasp how functions of two variables work, think of the coordinate system. The plane on which the x and y axes lie is where the function takes input, and the output z extends into the third dimension, often visualized as a surface.
For example, consider the function:
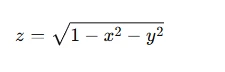
This function represents the upper hemisphere of a sphere. For this function to be valid, the expression under the square root must be non-negative, which leads to the condition x2+y2≤1. Hence, the domain of this function forms a circular disc in the x-y plane, and the range consists of values for z between 0 and 1, forming a spherical cap.
In this case, visualizing the function as a surface in three-dimensional space can help you understand the behavior of the function and its values for different points in the domain.
Practical Application: Solving Assignments Involving Functions of Two Variables
When solving assignments involving functions of two variables, you must understand both the theoretical and practical aspects. Start by familiarizing yourself with the concept of domains and ranges. Know how to determine whether a function is valid over a certain domain, and be able to visualize the function’s output.
- Interpretation: Always interpret the problem geometrically. For instance, if given a function like z=1−x2−y2, sketch the domain on the x-y plane and visualize the resulting surface.
- Identifying the Domain: Understand the constraints on the function. For example, the function z=1−x2−y2 has restrictions due to the square root. Always ask yourself what conditions must be true for the function to remain real.
- Computing the Range: Use algebraic reasoning to deduce the possible values of the function’s output. In the case above, the range is between 0 and 1 because x2+y2≤1.
The Concept of Limits in Functions of Two Variables
As we move to limits, recall that limits help us understand the behavior of a function as the input approaches a particular point. When dealing with functions of one variable, limits are often simpler to conceptualize because there’s only one variable to consider. However, the limit of a function of two variables can be trickier, as the behavior in two-dimensional space can vary depending on the path taken toward the point.
In this context, the limit of a function of two variables can be defined similarly to the limit of a function of one variable, but with additional considerations. Specifically, the limit must be the same no matter which path you approach the point from.
Limit of a Function of Two Variables
Consider a function f(x,y). We want to understand the limit of this function as (x,y) approaches a specific point, say (x0,y0). The limit is the value that f(x,y) approaches as (x,y) gets arbitrarily close to (x0,y0).
Mathematically, we write:
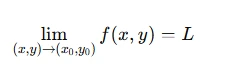
This means that for every small value of ϵ>0, there exists a corresponding δ>0 such that if (x,y) lies within a neighborhood around (x0,y0), the function's output will be within ϵ of L.
The Challenges of Working with Limits in Two Variables
When working on assignments related to limits of functions of two variables, several challenges may arise:
- Path Dependency: Unlike functions of one variable, the limit of a function of two variables may depend on the path taken to approach the point. For example, approaching (0,0) along the line x=y may yield a different result than approaching along the line x=−y. This is a major hurdle and is why it's essential to check the behavior of the function along different paths.
- Undefined Limits: There are cases where a function may not have a limit at a point. For instance, if the function exhibits different behaviors depending on the direction from which you approach the point, the limit does not exist.
- Visualizing Limits: It can sometimes be challenging to visualize the behavior of a two-variable function. A common strategy is to graph the function in three dimensions and look at how the surface behaves as the point is approached. This visualization helps in understanding how the function behaves near the point in question.
The Delta-Epsilon Definition of a Limit
To understand the limit of functions of two variables, we use a formal approach known as the delta-epsilon definition. The definition for the limit of a function of one variable states that:
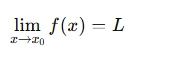
if for every ϵ>0, there exists a δ>0 such that whenever ∣x−x0∣<δ, we have ∣f(x)−L∣<ϵ.
This definition can be extended to two variables, where the distance between (x,y) and (x0,y0) is given by:
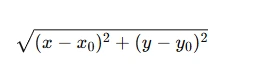
In the case of a function of two variables, for any given ϵ, you must find a corresponding δ such that whenever (x,y) is within δ of (x0,y0) the value of f(x,y) is within ϵ of L.
Solving Assignment Problems with Limits
When tackling assignments that ask you to compute limits, here's a step-by-step guide:
- Identify the Limit Point: The first step is to identify the point (x0,y0) at which the limit is to be evaluated.
- Check for Path Dependence: Explore different paths toward the point (x0,y0). Try to approach from different directions, such as along the line y=mx or along x=0x, to check if the limit is the same along all paths.
- Use the Delta-Epsilon Definition: Apply the delta-epsilon definition to prove that the limit exists. This involves finding an appropriate δ for a given ϵ.
- Visualize the Function: Use graphs to visualize the function’s behavior near the point. This can help confirm your results.
Conclusion
Functions of two variables can be a fascinating yet challenging topic in multivariable calculus. They involve understanding how two independent variables affect the dependent variable and how these relationships are represented mathematically. Mastering core concepts like the domain and range, as well as limits, is essential for building a strong foundation. The domain represents all possible input values, while the range refers to the set of output values, and limits help determine the behavior of the function as the input values approach certain points. However, as with any complex mathematical topic, functions of two variables present their own set of challenges. One of the most difficult aspects is dealing with path dependency when proving limits. This occurs when the value of a limit depends on the path taken toward a point, which can complicate the process of evaluating limits.
To approach assignments effectively, it’s crucial to visualize the problem geometrically. Graphs and contour maps can help provide a clearer understanding of the relationship between the variables. Additionally, a solid grasp of definitions, theorems, and their applications is necessary. With consistent practice and a methodical approach, you will improve your problem-solving skills and be able to apply these concepts in real-world scenarios, making complex problems easier to handle.