Effective Way to Approach Math Assignments on Taylor Polynomials and Taylor Series

Dr. Raymond Callister

Australia

Calculus

Dr. Raymond Callister, with over 12 years of experience in mathematical analysis and calculus, earned his Ph.D. from Western Sydney University, Australia.

Hire Me To Do Your Math Assignment

What Are Taylor Polynomials and Taylor Series?

To begin with, let’s explore what Taylor polynomials and Taylor series are. A Taylor polynomial is a finite sum used to approximate a function around a point x0. The polynomial provides an estimate of the function’s value near this point, which becomes increasingly accurate as the degree of the polynomial increases. A Taylor series, on the other hand, is the infinite sum of the terms of a Taylor polynomial, extending indefinitely to provide an exact representation of the function, provided the series converges.

Both concepts stem from Taylor's theorem, which generalizes the mean value theorem and plays a central role in analyzing the behavior of functions. Taylor’s theorem gives us a way to approximate a function using polynomials, making it easier to perform computations and derive insights, especially when direct computation with the original function is difficult.

Taylor Polynomials: An Intuitive Understanding

The fundamental idea behind Taylor polynomials is to construct a polynomial that matches a given function’s values and derivatives at a specific point x0. The degree of the polynomial determines how many derivatives of the function it matches.

Let’s break down the process. Suppose we have a function f(x), and we want to approximate it around a point x0​. The goal is to find a polynomial Pn(x) of degree n such that:

• The value of Pn(x) at x0​ equals f(x0),
• The first derivative of Pn(x) at x0 equals f′(x0),
• The second derivative of Pn(x) at x0​ equals f′′(x0),
• And so on, up to the n-th derivative.

This ensures that the polynomial approximates the function well at x0​. The higher the degree of the polynomial, the better the approximation near x0​. In practice, the polynomial captures the essence of the function’s behavior around that point.

Constructing a Taylor Polynomial

To construct a Taylor polynomial, we start by assuming a general polynomial form of degree n:

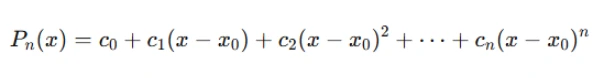
The coefficients c0,c1,…,cn​ are determined by the conditions imposed by the function and its derivatives at x0x_0x0​. For example, to find c0, we substitute x0​ into the polynomial and set it equal to the value of the function f(x0).

Next, we differentiate the polynomial and match the derivatives with those of the function at x0​. This will give us a system of equations that allows us to solve for the unknown coefficients. For instance, the first derivative of the polynomial at x0​ will match the first derivative of the function at x0​, and so on.

Understanding the Taylor Series

While the Taylor polynomial provides a finite approximation of a function, the Taylor series extends this idea to an infinite sum of terms. If the function is sufficiently smooth (i.e., it has derivatives of all orders), the Taylor series converges to the exact value of the function.

The Taylor series of a function f(x) around the point x0 is given by the infinite sum:

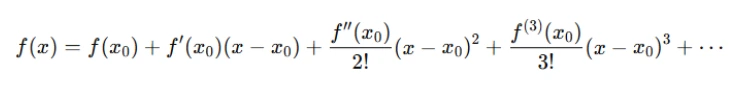
This series represents the function as the sum of its derivatives at x0​, weighted by factorials and powers of x−x0​. The more terms you include, the more accurate the approximation. In fact, for many functions, the Taylor series provides an exact representation.

However, it’s important to note that not all functions can be accurately represented by their Taylor series at every point. The series may not converge for all values of xxx, especially if the function has singularities or is not sufficiently smooth.

How to Apply Taylor Polynomials in Assignments

Now that we have a solid understanding of Taylor polynomials and Taylor series, the next step is to discuss how to apply these concepts to solve your math assignment on Taylor polynomials and series. The process typically involves:

1. Identifying the function: Determine which function needs to be approximated or analyzed using Taylor polynomials or Taylor series. This might be a function given in the problem statement, such as ex, sin(x), or cos(x).
2. Choosing the degree: Decide on the degree of the Taylor polynomial or series. In practice, you might be asked to compute the polynomial up to a certain degree (e.g., degree 3 or 4) or to find the Taylor series expansion.
3. Differentiating the function: Compute the required derivatives of the function at x0​. If you're working with a polynomial, remember that the derivatives should match at x0 up to the specified degree.
4. Forming the polynomial or series: Once you have the derivatives, use them to construct the Taylor polynomial or series. Pay attention to the factorial terms in the series, as they play a crucial role in the accuracy of the approximation.
5. Checking the remainder: If your assignment asks for the error or remainder of the approximation, compute the remainder term Rn(x) for the Taylor polynomial. This will give you an idea of how close your approximation is to the actual function.

Common Challenges in Solving Taylor Polynomial and Series Problems

While Taylor polynomials and series are powerful tools, they do present certain challenges that you may encounter when working on assignments. Some of the most common challenges include:

• Differentiation complexity: Some functions can have high-order derivatives that are difficult to compute. For example, functions like ex are simple, but others, like ln(x), may require careful differentiation.
• Convergence issues: For Taylor series, the series may not converge for all values of x. Determining the radius of convergence can be tricky and may require the application of convergence tests.
• Choosing the correct point: In practice, choosing the right point x0​ around which to expand the series or polynomial can affect the accuracy of the approximation. Sometimes the point of expansion is not explicitly given, and you'll need to choose a point based on the context of the problem.
• Handling higher-order terms: Higher-order terms in the Taylor series or polynomial can lead to more complex calculations, especially when the function has many derivatives. You’ll need to carefully compute each derivative and manage the terms.

Conclusion

Taylor polynomials and Taylor series are essential tools in calculus, allowing us to approximate complex functions and solve real-world problems. Understanding the theory behind these concepts and knowing how to apply them in assignments is crucial for success in mathematics. While you may face challenges, such as dealing with higher-order derivatives or convergence issues, practice and careful attention to detail will help you master these techniques. Whether you are approximating functions or analyzing their behavior, Taylor polynomials and Taylor series provide valuable insights that will aid you in your mathematical journey.

By mastering Taylor polynomials and series, you’ll be equipped to tackle a wide variety of problems and gain a deeper understanding of how functions behave in different contexts. Keep practicing, and you’ll soon become confident in handling these assignments with ease.