How to Tackle and Solve Math Assignments on Double Integrals

Double integrals extend single-variable integration to two dimensions and are essential in calculus for computing areas, volumes, and other properties over a given region in the xy-plane. They are widely used in physics, engineering, and probability. However, university students often struggle with double integrals due to their complexity in setup, evaluation, and interpretation. Understanding double integrals requires mastering concepts like iterated integration, limits of integration, and changing order of integration. It is crucial to practice solving problems using Cartesian and polar coordinates to develop problem-solving skills.
Assignments on double integrals often involve computing areas under surfaces, finding volumes of solids, or solving real-world problems involving mass and center of mass. The biggest challenges students face include determining integration limits, selecting appropriate coordinate systems, and handling complex integrals. To study effectively, students should focus on visualization techniques, breaking problems into simpler steps, and using computational tools when necessary. Practicing different types of problems and understanding their real-world applications can also improve comprehension. By mastering double integrals, students can complete their math assignment and enhance their calculus skills to tackle more advanced mathematical problems with confidence.

Understanding the Concept of Integration
Before diving into double integrals, it is important to recall the basic idea behind single-variable integration. A definite integral of a function f(x) over an interval [a,b] represents the area under the curve of the function between these limits.
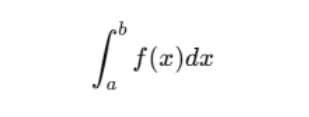
This integral is defined as the limit of a sum, where the interval [a,b] is divided into small subintervals, and the function value is multiplied by the width of each subinterval. When the number of subintervals approaches infinity, the sum converges to the exact area.
Double integrals extend this idea to two dimensions, where the function f(x,y) is integrated over a region D in the xy-plane. Instead of summing up small line segments, we sum up small regions (rectangles or other shapes) to compute the total contribution over the domain.
Defining Double Integrals
A double integral is used to integrate a function of two variables over a region in the xy-plane. Given a function f(x,y), its double integral over a region D is expressed as:
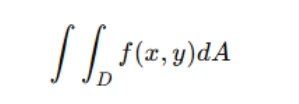
Here, dA represents the area element of a small subregion in D, which can be written as dxdy, depending on how the integral is evaluated. The integral sums up the function values multiplied by the infinitesimal area elements, ultimately giving a total measure such as volume.
Geometric Interpretation
While single integrals compute the area under a curve, double integrals compute the volume under a surface. Imagine a function f(x,y) defining a surface above the xy-plane. The double integral sums up the contributions of small subregions of D, each contributing a small volume element. When all these elements are added together, we obtain the total volume under the surface.
How to Study Double Integrals for Assignments
Understanding double integrals requires a structured approach to studying. These integrals extend the concept of single-variable integration to two dimensions, making them essential in fields like physics, engineering, and probability. To grasp them effectively, start by reviewing the fundamentals of integration and functions of multiple variables. Visualizing regions of integration helps in setting up limits correctly. Mastering iterated integrals, where one variable is integrated first while treating the other as constant, is crucial. Changing the order of integration and using coordinate transformations, such as polar coordinates, simplifies complex problems. Practice is key—solving different types of problems enhances understanding. Additionally, applications like finding areas, volumes, and mass distributions provide practical insights. Using graphical tools and software can also aid in comprehension.
A step-by-step approach, along with consistent practice, ensures a strong grasp of double integrals and their applications in real-world scenarios. Here are key steps to master them effectively:
- Review Basic Integration Concepts
- Understand the Limits of Integration
- Practice Setting Up the Integral
- Evaluate the Integral Step by Step
- Work on Visualizing the Region
Since double integrals build upon single-variable integration, it is essential to have a strong foundation in definite integrals. Revise properties of integrals, substitution techniques, and the Fundamental Theorem of Calculus.
The limits of integration define the region D over which the function is integrated. These limits can be constant (rectangular regions) or variable (general regions bounded by curves). Visualizing the domain is crucial for setting up the correct integral.
A major challenge in solving double integrals is correctly setting up the integral based on the given region. Identifying whether to integrate first with respect to x or y, and determining the appropriate limits, is key to solving problems accurately.
Double integrals are evaluated iteratively. First, integrate with respect to one variable while treating the other as a constant, then integrate the resulting expression with respect to the second variable. Breaking down the problem into simpler steps helps in solving it correctly.
Sketching the region of integration helps in understanding the limits and choosing the correct order of integration. Many mistakes in double integrals arise from incorrect limits, which can be avoided by carefully analyzing the region.
Application of Double Integrals in Assignments
Double integrals are a fundamental concept in calculus and frequently appear in university assignments across mathematics, physics, and engineering courses. These integrals are used to calculate areas, volumes, mass, and other physical properties over two-dimensional regions. Depending on the problem, students may need to set up double integrals in Cartesian or polar coordinates, carefully defining limits based on the given region. Some problems involve straightforward rectangular domains, while others require transformation techniques to simplify complex boundaries. Additionally, applications of double integrals extend to probability, fluid dynamics, and heat transfer, making them essential for real-world problem-solving. Assignments may ask students to evaluate double integrals analytically or numerically, emphasizing the importance of understanding integration techniques such as Fubini’s theorem and iterated integration. Mastering double integrals requires a strong grasp of function behavior, region interpretation, and computational methods, making them a challenging yet crucial topic in higher-level mathematics courses. Here are some common applications:
- Finding Areas of Regions
- Computing Volumes Under Surfaces
- Evaluating Mass and Density Problems
- Centroids and Moments of Inertia
By setting the function f(x,y)=1, the double integral simply computes the area of the region D. This is a fundamental application often used in geometry and physics problems.
One of the most common uses of double integrals is to calculate the volume of a solid under a given surface z=f(x,y). This is widely applied in physics and engineering problems involving three-dimensional structures.
If a lamina (thin sheet) has a density function ρ(x,y), its mass can be computed using:
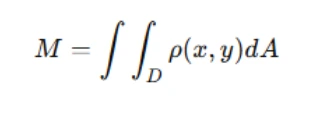
This principle is used in mechanical engineering and physics applications.
In mechanics, double integrals help compute centroids, moments of inertia, and center of mass, which are essential for analyzing stability and motion of objects.
Common Challenges and How to Overcome Them
One common challenge students face with double integrals is setting up the correct limits of integration. This can be overcome by carefully analyzing the given region and sketching it to determine the order of integration. Another difficulty is choosing between Cartesian and polar coordinates. When dealing with circular or radial regions, converting to polar coordinates simplifies calculations. Computational errors, especially when integrating complex functions, can also be an issue. To avoid mistakes, break the problem into smaller steps and verify results at each stage. Understanding the geometric interpretation of double integrals is another challenge. Visualizing the region and how integration accumulates area or volume can provide better insight. Finally, lack of practice often leads to confusion. Regularly solving problems and revisiting fundamental concepts helps reinforce understanding. Seeking help from textbooks, online resources, or instructors can also provide valuable guidance when struggling with specific problems. Here are the most effective strategies to tackle these challenges and master double integrals.
- Understanding the Limits of Integration
- Choosing the Right Order of Integration
- Handling Complex Functions
- Interpreting Word Problems Correctly
- Avoiding Computational Mistakes
One of the biggest difficulties students face is setting up the correct limits of integration. This problem can be tackled by carefully sketching the region and determining the boundaries for x and y.
Sometimes, changing the order of integration makes the problem easier to evaluate. If one order leads to difficult computations, try switching the order and simplifying the limits accordingly.
Some functions involve complicated algebraic expressions, making integration difficult. In such cases, recognizing patterns, using substitution techniques, or applying symmetry properties can help simplify the process.
Assignments often frame problems in a real-world context, requiring students to extract the correct mathematical formulation. Carefully identifying what is being asked and translating it into an appropriate double integral setup is key to solving such problems.
Since double integrals involve multiple steps, errors in basic calculations can lead to incorrect results. Always verify each step, simplify expressions before integrating, and double-check limits to minimize mistakes.
Conclusion
Double integrals are a crucial mathematical tool used in various fields, from geometry to physics and engineering. Mastering them requires a clear understanding of their definition, properties, and applications. By systematically studying integration techniques, practicing problem setups, and developing a strong conceptual grasp, students can handle double integral assignments with confidence.
Despite the challenges, with the right approach—visualizing regions, carefully setting up limits, and evaluating iteratively—solving problems involving double integrals becomes manageable. By focusing on these strategies, university students can improve their problem-solving skills and successfully complete their assignments on double integrals.