How to Handle Math Assignments on System of Linear Equations

Linear algebra is a cornerstone of mathematics, and one of its most fundamental concepts is the system of linear equations. Whether you're studying engineering, computer science, economics, or physics, understanding how to solve these systems is crucial. A system of linear equations consists of multiple equations that share a common set of variables, and the goal is to find values for these variables that satisfy all equations simultaneously. Systems can have a unique solution, infinitely many solutions, or no solution, depending on the relationships between the equations.
In this blog, we’ll explore the theoretical foundations of linear equations, their geometrical interpretations, and practical applications. For instance, in two dimensions, each equation represents a line, and the solution corresponds to the point(s) where these lines intersect. We’ll also discuss challenges students often face, such as handling large systems, understanding matrix representations, and interpreting inconsistent or infinite solutions.

Additionally, we’ll provide tips on how to study effectively, solve assignments, and apply these concepts to real-world problems. By the end, you’ll have a solid grasp of how to solve your math assignment related to systems of linear equations with confidence and precision. Whether you're solving a simple 2-variable system or a complex multi-equation problem, this guide will equip you with the tools to excel.
Introduction to the System of Linear Equations
A system of linear equations consists of multiple linear equations that share a common set of variables. The goal is to find values for these variables that satisfy all the equations simultaneously. For example, consider the following system:
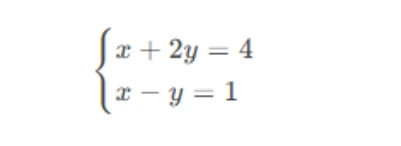
Here, x and y are the variables, and the equations are linear because each term is either a constant or the product of a constant and a single variable. The system can have one of three possible outcomes: a unique solution, infinitely many solutions, or no solution. Understanding these possibilities is key to solving systems of linear equations effectively.
Geometrical Interpretation of Linear Equations
To visualize a system of linear equations, let’s consider the case of two variables, x and y. Each equation in the system represents a straight line on a 2D plane. The solution to the system corresponds to the point(s) where these lines intersect.
When two lines intersect at a single point, the system has a unique solution. For example, the lines x+2y=4 and x−y=1 intersect at the point (2,1), which is the unique solution. This is the most straightforward case and often the one students encounter first.
However, not all systems have a unique solution. If the two lines are parallel and never intersect, the system has no solution. For instance, the lines x−y=1 and −x+y=2 are parallel and do not intersect, meaning the system has no solution. This scenario can be confusing, especially when dealing with real-world problems where a solution is expected.
On the other hand, if the two lines are identical (i.e., one equation is a multiple of the other), every point on the line is a solution. For example, the lines x−y=2 and −x+y=−2 are the same line, so the system has infinitely many solutions. This case requires a different approach, as the solution set is not a single point but an entire line.
This geometrical interpretation can be extended to systems with more variables. For instance, in three dimensions, each equation represents a plane, and the solution corresponds to the intersection of these planes. Understanding this visualization helps in grasping the concept of solutions in higher dimensions.
Challenges in Solving Systems of Linear Equations
While the concept of linear equations is straightforward, solving them can be challenging, especially as the number of variables and equations increases. One of the primary challenges is identifying the type of solution. Determining whether a system has a unique solution, no solution, or infinitely many solutions requires careful analysis of the equations and their relationships. This step is crucial because it dictates the approach you’ll take to solve the system.
Another challenge is handling large systems. As the number of variables and equations grows, solving the system manually becomes time-consuming and error-prone. Techniques like matrix operations and computational tools become essential in such cases. However, these methods require a solid understanding of matrix algebra, which can be intimidating for beginners.
Understanding matrix representations is another hurdle. Representing a system of equations in matrix form (Ax=b) is a powerful tool, but it requires familiarity with concepts like matrix multiplication, determinants, and inverses. Students often struggle with these topics, especially when transitioning from simple systems to more complex ones.
Dealing with inconsistent systems (those with no solution) can also be confusing, particularly when they arise in real-world applications. Recognizing and interpreting such systems is a critical skill that takes time to develop. Similarly, when a system has infinitely many solutions, expressing the solution set clearly can be challenging. This often involves introducing parameters to describe the solution space, which adds another layer of complexity.
How to Study and Apply Linear Equations in Assignments
To master systems of linear equations and excel in your assignments, it’s essential to adopt a structured approach. Start by understanding the basics. Review the fundamentals of linear equations, including their forms and properties. Practice solving simple systems with two variables to build intuition and confidence. This foundational knowledge will serve as a springboard for tackling more complex problems.
Next, learn multiple solution methods. Familiarize yourself with different techniques for solving systems of linear equations, such as the substitution method, elimination method, and matrix methods. Each method has its strengths and is suited to different types of problems. For example, the substitution method is ideal for small systems, while matrix methods like Gaussian elimination are more efficient for larger systems.
Practicing geometrical interpretation is another valuable strategy. Visualize systems of equations by plotting them on a graph. This will help you understand the relationships between equations and their solutions. For instance, seeing how two lines intersect or run parallel can provide insights into the nature of the solution.
Applying your knowledge to real-world problems is equally important. Linear equations are used in various fields, from optimizing resources in engineering to analyzing economic models. Working on practical problems will deepen your understanding and make the concepts more relatable. It will also prepare you for assignments that require you to apply linear algebra to real-world scenarios.
Using computational tools can save time and reduce errors, especially when dealing with large systems. Software like MATLAB, Python (NumPy), or graphing calculators can handle complex calculations efficiently. However, it’s crucial to understand the underlying principles before relying on these tools.
Finally, review and reflect on your work. After solving a problem, go through your steps to ensure accuracy. Reflect on the challenges you faced and how you overcame them. This self-assessment will help you identify areas for improvement and reinforce your learning.
Practical Tips for Handling Assignments
When working on assignments, start by reading the problem carefully. Understand what is being asked before jumping into calculations. Misinterpreting the problem can lead to incorrect solutions, even if your calculations are accurate.
Organize your work to avoid confusion. Write down the equations clearly and label them. This will make it easier to follow your thought process and identify any mistakes. If you’re using matrices, ensure that they are set up correctly and that each step is documented.
Before solving, check for consistency. Analyze the system to determine if it has a unique solution, no solution, or infinitely many solutions. This preliminary analysis will guide your approach and save time.
Once you’ve found a solution, verify it by substituting the values back into the original equations. This step is crucial for ensuring that your solution satisfies all the equations in the system.
If you’re stuck, don’t hesitate to seek help. Consult your professor, classmates, or online resources. Sometimes, a different perspective can make a challenging problem more manageable.
Conclusion
The system of linear equations is a foundational topic in linear algebra with wide-ranging applications. By understanding its theoretical underpinnings, practicing problem-solving techniques, and applying your knowledge to real-world scenarios, you can master this essential concept. Remember, the key to success is consistent practice and a willingness to tackle challenges head-on. Whether you’re solving a simple 2-variable system or a complex multi-equation problem, the skills you develop will serve you well throughout your academic and professional journey.
So, the next time you encounter a system of linear equations in your assignments, approach it with confidence. Break it down step by step, visualize the problem, and apply the appropriate solution method. With time and practice, you’ll find that solving these systems becomes second nature. Happy studying!